Style tranform

图像风格迁移

Overview ¹:

1. Create a random input image

2. Pass the input through a pretrained backbone architecture say VGG, ResNet(note that this backbone will not be trained during backpropagation).

3. Calculate loss and compute the gradients w.r.t input image pixels.Hence only the input pixels are adjusted whereas the weights remain constant.

注意几点：卷积神经网络只是用来提取image特征，起embedding作用。所以作为主干的卷积神经网络并不用来训练，我们更多的是反向传播更改输入的random图像。

最终我们生成的图片需要达到两个目的：

• 包含 content image 的内容，比如说有狗，猫，或是固定的建筑物等，至于物体的纹理、颜色等特征我们是不需要保持等，这一部分是风格来保证。

• 包含 style image 的风格，比如说画家的绘画手法，竖条纹理喜欢用热烈的橘色，波浪形的线条习惯画的很浓重且颜色为冷色调等。

Learning Content

对于内容学习：我们要如何设计target和input才能保证只学到“内容”而不拷贝“风格”？这一点很关键，所以这里使用了feature Map:

Convolutional feature maps are generally a very good representation of input image’s features. They capture spatial information of an image without containing the style information(if a feature map is used as it is), which is what we need. And this is the reason we keep the backbone weights fixed during backpropagation.

卷积层的选择：

Using feature maps of early conv layers represent the content much better, as they are closer to the input, hence using features of conv2, conv4 and conv7.

Learning Style

这里用到Gram矩阵，其会衡量k个向量之间的关系。说到两个向量的度量，向量积的含义需要提一下：

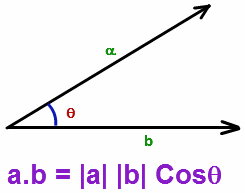
In a more intuitive way, dot product can be seen as how similar two vectors actually are.

当我们把某个卷积层的feature Map展开(flat)成vector时，其就可以看作一个feature vector，这样如果对于[width, height, channel] = [w, h, c] 这样一个卷积层，我们会得到c个feature vector，如果图片记作$X$,

$$f(X) = \alpha_1, \alpha_2, … , \alpha_c$$

这样一来，每一对向量之间作向量点乘就会衡量不同特征之间的关系，比如说一个向量代表冷色调，另一个代表粗线条，这两个向量的点乘约大说明约相近，可以理解为这两种特征经常一起出现，即代表一种风格。

Consider two vectors(more specifically 2 flattened feature vectors from a convolutional feature map of depth C) representing features of the input space, and their dot product give us the information about the relation between them. The lesser the product the more different the learned features are and greater the product, the more correlated the features are. In other words, the lesser the product, the lesser the two features co-occur and the greater it is, the more they occur together. This in a sense gives information about an image’s style(texture) and zero information about its spatial structure, since we already flatten the feature and perform dot product on top of it.*

格拉姆矩阵可以看做feature之间的偏心协方差矩阵（即没有减去均值的协方差矩阵），在feature map中，每个数字都来自于一个特定滤波器在特定位置的卷积，因此每个数字代表一个特征的强度，而Gram计算的实际上是两两特征之间的相关性，哪两个特征是同时出现的，哪两个是此消彼长的等等，同时，Gram的对角线元素，还体现了每个特征在图像中出现的量，因此，Gram有助于把握整个图像的大体风格。有了表示风格的Gram Matrix，要度量两个图像风格的差异，只需比较他们Gram Matrix的差异即可²。

总之， 格拉姆矩阵用于度量各个维度自己的特性以及各个维度之间的关系。内积之后得到的多尺度矩阵中，对角线元素提供了不同特征图各自的信息，其余元素提供了不同特征图之间的相关信息。这样一个矩阵，既能体现出有哪些特征，又能体现出不同特征间的紧密程度²。

gram矩阵：

定义：$n$ 维欧氏空间中任意$k(k \le n)$ 个向量$\alpha_1, \alpha_2, … ,\alpha_k$ 的内积所组成的矩阵

$$\begin{equation} \Delta\left(\alpha_{1}, \alpha_{2}, \ldots, \alpha_{k}\right)=\left(\begin{array}{cccc}{\left(\alpha_{1}, \alpha_{1}\right)} & {\left(\alpha_{1}, \alpha_{2}\right)} & {\dots} & {\left(\alpha_{1}, \alpha_{k}\right)} \\ {\left(\alpha_{2}, \alpha_{1}\right)} & {\left(\alpha_{2}, \alpha_{2}\right)} & {\ldots} & {\left(\alpha_{2}, \alpha_{k}\right)} \\ {\cdots} & {\cdots} & {\cdots} & {\ldots} \\ {\left(\alpha_{k}, \alpha_{1}\right)} & {\left(\alpha_{k}, \alpha_{2}\right)} & {\ldots} & {\left(\alpha_{k}, \alpha_{k}\right)}\end{array}\right) \end{equation}$$

称为$k$个向量的格拉姆矩阵（Gram matrix)，其行列式称为Gram行列式。

¹. https://towardsdatascience.com/neural-networks-intuitions-2-dot-product-gram-matrix-and-neural-style-transfer-5d39653e7916 ↩

². https://blog.csdn.net/wangyang20170901/article/details/79037867 ↩